Alain JUGE : Contribution sur les fusées à eau

Aerodynamique

Il n'est ni dans mes ambitions, ni même, hélas, dans mes compétences, de faire ici un cours sur l'aerodynamique. Toutefois, nous verrons un certain nombre de notions indispensables pour bien comprendre le comportement d'une fusée dans l'air.

Pour en savoir plus on pourra, notamment, se reporter à l'article Wikipedia sur l'aerodynamique.

Les fusées dont il est question ici évoluent dans l'atmosphère terrestre communément appelée l'air. L'air est un gaz (ou plus précisément un mélange de gaz) qui est donc compressible, expansible, élastique, visqueux et aussi pesant. Toutes ces caractéristiques ont une influence sur le déplacement des solides dans l'air.

L'aérodynamique est l'étude du comportement de l'air sur les corps en mouvement.

L'écoulement de l'air le long d'un corps, que ce soit l'air qui se déplace ou le corps, peut se faire selon deux régimes :

• Le régime laminaire, où toutes les molécules d'air suivent des trajectoires parallèles. Toutefois, les molécules en contact avec le corps en mouvement ont une vitesse nulle par rapport à celui-ci, puis les couches (ou lames) d'air un peu plus éloignées auront une vitesse supérieure. Enfin à partir d'une certaine distance du corps en mouvement, toutes les couches d'air auront la même vitesse, la vitesse propre du flux d'air. L'ensemble des couches d'air dont la vitesse est inférieure à la vitesse du flux, constitue la couche limite.
• Le régime turbulent, où les molécules d'air suivent des trajectoires désordonnées, tout en étant entraînée dans un flux global ayant une vitesse propre.

On retrouve ces deux types d'écoulement en hydrodynamique, il existe des cours d'eau qui traversent des zones peu pentues et sans obstacles (la Seine par exemple), l'écoulement de l'eau est laminaire, puis il y a d'autres cours d'eau à plus forte pente, avec des rochers dans leur lit et où l'eau s'écoule de façon plus tourmentée (torrent), leur écoulement est en régime turbulent.

Si nous considérons maintenant un flux d'air laminaire et que l'on place dans ce flux d'air une plaque plane perpendiculairement à ce flux. L'expérience peut être faite avec un ventilateur et une pochette de CD par exemple.

Les filets d'air qui arrivent sur la plaque ne vont plus pouvoir continuer leur chemin et vont devoir contourner cette plaque. Toutefois, ces filets d'air vont exercer une pression sur la plaque, faites l'expérience : devant un ventilateur placez une pochette de CD, vous sentirez la force exercée par la pression de l'air sur la pochette.

Mais les filets d'air détournés vont avoir tendance à continuer leur chemin parallèlement au sens d'écoulement, créant ainsi un vide d'air, « une dépression », derrière la plaque. Mais « la nature ayant horreur du vide », les molécules d'air (et la plaque aussi d'ailleurs) vont être aspirées par cette dépression créant ainsi un régime turbulent derrière la plaque.

On visualiserait mieux le phénomène dans une rivière, dans une portion ou l'écoulement est laminaire, si on place un caillou en travers du courant, on voit bien que l'eau vient buter sur ce caillou, créant une remontée du niveau d'eau devant, alors que derrière, se créent des tourbillons.

Si maintenant nous plaçons la pochette de CD parallèlement au flux d'air du ventilateur.

La pochette étant mince, le flux d'air sera peu perturbé, toutefois on sent qu'une force tend à éloigner cette pochette du ventilateur. Cette force est essentiellement due au frottement de l'air sur les parois de la pochette. En effet, le fait que les couches d'air à proximité des parois de la pochette aient des vitesses différentes va créer des forces de viscosité, qui peuvent être importantes.

L'ensemble des forces dues à ces trois phénomènes (pression à l'avant, dépression à l'arrière et frottements) constitue la résistance de l'air.

Cette résistance de l'air est fonction :

• De la densité de l'air ? en kg.m^-3
• De la surface S que présente le mobile face au flux d'air, appelée maître couple en m²
• Du carré de la vitesse V en m.s^-1
• De la forme du mobile pour lequel on défini un coefficient de pénétration dans l'air Cx (sans dimension)

Ce qui se traduit par la relation :

R étant une force, elle est exprimée en N.

Revenons sur ce qu'il est convenu d'appeler le Maître couple. C'est donc la surface S que présente le mobile face au flux d'air, c'est donc la projection du corps placé dans le flux d'air sur un plan perpendiculaire au flux.

Dans les deux exemples précédents, si l'on considère qu'une pochette de CD a pour dimension 12x12x0,5 cm. Lorsqu'elle est perpendiculaire au flux d'air, son maître couple vaut 12 x 12 = 144 cm², dans le deuxième cas il vaudra 12 x 0,5 = 6 cm². Pour une fusée de diamètre D ayant 4 ailerons d'envergure L et d'épaisseur e, si celle-ci est parfaitement dans l'axe du flux d'air, son maître couple sera :

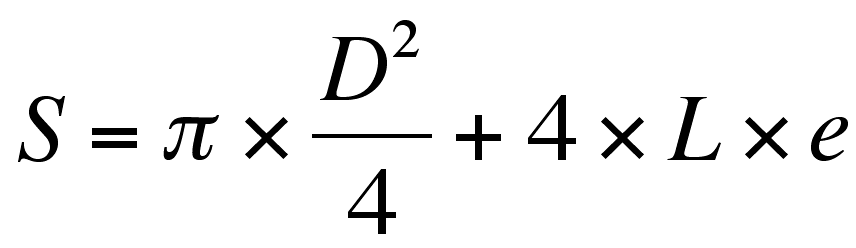
Précédemment, nous avons vu le cas d'une plaque disposée soit perpendiculairement au flux d'air, soit parallèlement. Mais que se passe-t-il, si la plaque fait un angle ? avec le flux d'air ?

Comme dans le cas de la surface perpendiculaire, il va se produire un phénomène de surpression sur la surface frappée par le flux d'air et une dépression sur la surface « à l'abri ». D'autre part la plaque est aussi soumise à une force de frottement. Cette surpression, cette dépression et cette force de frottement vont s'additionner pour constituer la résistance de l'air. A noter que la force résultante de la dépression est environ 3 fois plus importante que celle due à la surpression et que la force de frottement est généralement faible devant les deux autres.

Cette résistance de l'air s'applique de façon perpendiculaire à la plaque en un point nommé centre de poussée, comme celle-ci fait un angle ? (appelé angle d'incidence) avec le flux d'air, on peut décomposer cette force en deux autres forces, l'une dans l'axe du flux d'air et l'autre perpendiculaire.

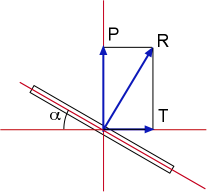
La composante T dans l'axe du flux d'air s'oppose à l'avancement de la plaque, c'est la force de traînée. La composante P perpendiculaire au flux d'air tend à faire monter la plaque, c'est la force de portance.

Pour nos fusées à eau, il faudra tenir compte de ces deux forces :

• La force de traînée va s'opposer à l'avancement, aussi pour avoir des performances maximum, il faudra s'attacher à diminuer autant que possible cette traînée. Ce sera obtenu en travaillant la forme de l'engin (autrement dit le Cx) pour qu'il présente le moins possible d'aspérités génératrices de turbulences, en limitant autant que faire se peut le maître couple (éviter les ailerons d'envergure gigantesque et très épais) et enfin en évitant que la fusée prenne trop d'incidence.
• La force de Portance va permettre d'assurer la stabilité de la fusée en la ramenant parallèle au flux d'air chaque fois qu'une perturbation tentera de l'en dévier.

Voyons maintenant le comportement de la fusée complete en vol.

Les forces qui s'exercent sur cette fusée sont :

• la poussée (au moins dans un premier temps) qui s'exerce dans l'axe de la fusée et dont le point d'application se situe au centre de gravité.
• le poids qui s'exerce verticalementet dont le point d'application se situe également au centre de gravité.
• la résistance de l'air qui s'exerce dans l'axe du flux d'air autour de la fusée et qui s'applique en un point appelé "centre latéral de poussée" ou CLP

Le schéma ci-dessous resume ce bilan de forces.

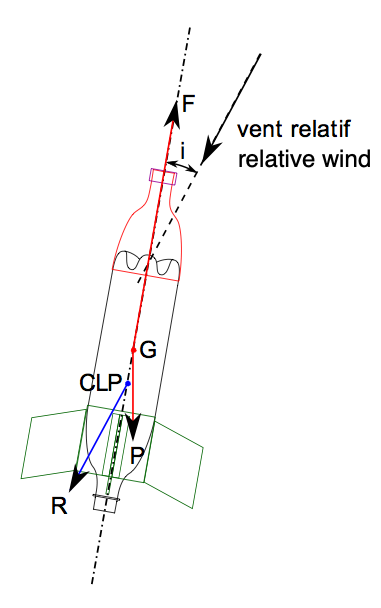
Sur ce schéma F est la force de poussée, R est la résistance de l'air et P le poids (soit la masse multipliée par l'accélération de la pesanteur : m*g). G est le centre de gravité de la fusée et CLP est le centre latéral de poussée.

Nous avons également indiqué le sens du "vent relatif", qui fait un angle i avec l'axe de la fusée. De quoi s'agit-il ?

Quand la fusée se déplace dans l'air,il y a deux phénomènes qui entre en jeu :

• le déplacement "naturel" de l'air lié aux conditions météorologiques et que l'on appelle le vent vrai et qui est généralement horizontal (parallèle à la surface de la terre)
• le déplacement de la fusée dans l'air et qui crée ce que l'on appelle un vent propre (ça ne veut pas dire qu'il est exempt de toute impureté, mais que c'est le vent de la fusée, donc qui lui appartient). Ce vent propre est évidemment dans l'axe de la vitesse de la fusée.

La combinaison de ces deux vents constitue le vent relatif. Et c'est ce vent relatif qui exerce sur la fusée des forces aerodynamique appellée globalement la résistance de l'air.

Pour comprendre comment vont agir les différentes forces qui s'appliquent sur notre fusée, nous allons, chacune, les décomposer en forces axiale et normale. La force axiale s'applique le long de l'axe de la fusée et la force normale s'applique perpendiculairement à cet axe.

Notons tout de suite que la poussée s'exerçant dans l'axe de la fusée, sa composante normale est nulle. Nous nous interesserons donc essentiellement aux deux autres forces que sont la résistance de l'air et le poids. Le schéma ci-dessous nous indique ces décompositions.

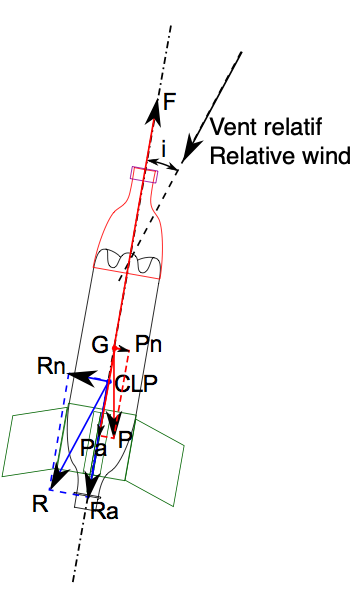
Donc ici, le poids P est décomposé en Pn (composante Normale) et Pa (composante axiale), de même R est décomposée en Rn (composante Normale) et Ra (composante axiale). Ra est appellée la Trainée, tandis que Rn est appellée la Portance

Les composantes axiales vont s'opposer au déplacement de la fusée, tandis que les forces normales vont contribuer à la stabilité (ou l'instabilité) de la fusée, et c'est ce que nous allons étudier de plus près maintenant.

Pour y voir plus clair, nous allons oublier tout ce qui ne nous sert à rien dans cette étude et ne garder que les forces normales. D'où le schéma ci dessous :

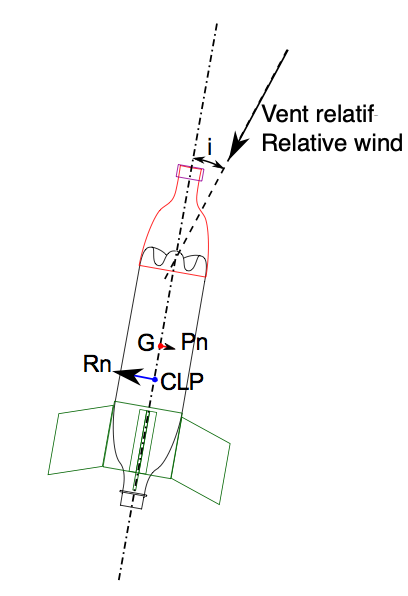
L'angle i que fait l'axe de la fusée avec le vent relatif s'appelle l'angle d'incidence. On a vu précédemment que la résistance de l'air était égale à

Donc pour Rn (la portance), Cx est appellé Cn coefficient de portance et S est la surface de la fusée projetée sur un plan perpendiculaire au vent relatif. On voit bien que plus l'angle d'incidence sera grand et plus cette surface sera grande donc Rn sera grande.

On voit aussi sur le schéma ci-dessus que Rn et Pn créent un couple qui tend à ramener la fusée dans l'axe du vent relatif, c'est à dire à réduire l'angle d'incidence. Ce qui signifie que si une perturbation quelconque dévie la fusée de l'axe du vent relatif, la force de portance la ramenera dans cet axe. Sauf que, sur le schéma ci-dessus, nous sommes dans une bonne configuration. En effet, supposons que, par exemple, la fusée n'ait pas d'ailerons et que sa masse soit principalement localisée dans le bas (cas d'une fusée à eau au décollage). Alors, le CLP sera plus haut et le centre de gravité plus bas. Que va-t-il se passer si la fusée s'écarte de sa route ?

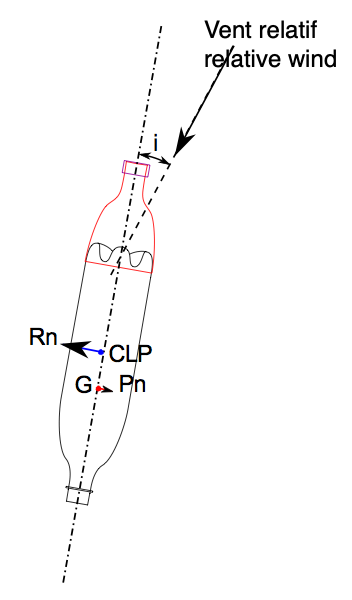On voit ici que l'effet du couple Rn/Pn va éloigner la fusée du vent relatif et aura tendence à se stabiliser à l'envers (le devant derrière). Mais s'il y a encore de la poussée, le retour prématuré au sol est évident, ce qui l'est moins, c'est où ce retour va se faire. Donc ce sont des conditions très dangereuses qu'il faut éviter à tout prix.

Mais, revenons à notre cas précédent où le CLP est sous le CdG, condition impérative pour avoir une fusée stable.

Dans la pratique, si la vitesse est suffisante, Pn est faible devant Rn, ce qui implique que le centre de rotation lié à ce couple est proche du centre de gravité. On peut donc considérer que la "vivacité" de réaction à une déviation inopinée de trajectoire est liée au produit de Rn (la portance) par la distance Centre de gravité- centre Latéral de poussée. Cette distance, divisée par le diamètre de la fusée est appellé : marge statique.

Pour une bonne stabilité de la fusée la marge statique doit être supérieure à 1.