La stabilité des fusées à eau
Nous avons vu à la page consacrée à l'aerodynamique qu'il était necessaire d'avoir le Centre Latéral de poussée sous le centre de gravité. Ce que nous n'avons pas vu par contre, c'est comment déterminer où se trouvent les centres de gravité et de poussée, ni comment faire évoluer leur position si elles ne sont pas correcte. C'est ce que nous allons voir ici.
Les fusées à eau présentent quelques particularités qu?il faut souligner.
La « masse propulsive » est en rapport beaucoup plus importante que pour les fusées à poudre, par exemple une fusée à eau constituée d?une bouteille de 1,5l va peser à vide environ 100 g, mais remplie avec 1/3 de volume d?eau, elle va peser 600g. Une mini-fusée avec moteur cariacou pèsera environ 1,2kg à vide pour une masse de poudre de 70g. Ceci explique la formidable accélération des fusées à eau.
Cela signifie, aussi, que le centre de gravité de la fusée va énormément se déplacer pendant la phase de propulsion. Il va remonter, ce qui est plutôt favorable pour la stabilité, heureusement d?ailleurs puisqu?une fusée à eau au décollage, donc avec toute l?eau à l?intérieur, a son centre de gravité très bas (grosso modo c?est le centre de gravité de la masse d?eau) donc pour avoir un centre de poussée plus bas d?au moins un diamètre, cela nécessite des ailerons très grands ou/et très bas.
En pratique, la phase de propulsion étant généralement très courte, quelques centième de secondes, il n?est pas nécessaire d?avoir une fusée stable au décollage. D?une part, la masse d?eau va se libérer très vite donc la durée d?instabilité sera très courte et s?il y a une perturbation au décollage, très vite la fusée retrouvera sa trajectoire, d?autre part l?accélération est énorme ce qui veut dire que la vitesse est rapidement importante donc l?effet aérodynamique des ailerons sera rapidement sensible.
Pour autant, il faut bien garder en mémoire que le décollage peut être périlleux et qu?il est donc impératif d?observer les règles élémentaires de sécurité lors des lancements. Ce fait milite aussi en faveur d?un guidage de la fusée au décollage.
Enfin, la durée de la phase de propulsion est fonction du diamètre de la tuyère, plus le diamètre est petit, plus la durée sera longue et donc la période d?instabilité grande. Plus le diamètre de tuyère sera faible, plus il sera nécessaire de concevoir un engin stable même en charge, ce qui malheureusement ne peut se faire qu?au détriment des performances.
Mais la vie est ainsi faite, tout est affaire de compromis...
Le grand principe, qui permet de déterminer si une fusée sera stable ou non, dit que :
Le centre de gravité doit se trouver au dessus du centre latéral de poussée, d?au moins un calibre.
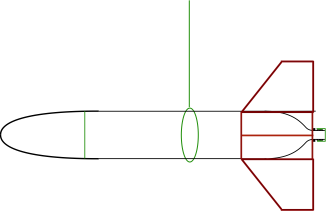
Le centre de gravité est le point d?application du poids, il est donc facile de déterminer expérimentalement sa position pour la fusée à vide. Il suffit en effet de suspendre la fusée, à l?aide d?une ficelle passée autour de son fuselage et de rechercher le point où elle restera horizontale. La position de la ficelle indiquera celle du centre de gravité (CdG).
Malheureusement cette technique ne permet pas de trouver le centre de gravité avec l?eau à l?intérieur puisque celle-ci se répand horizontalement. Il faudra donc le calculer , sachant que :
si l?on appelle Xv, Xe et Xg les distances du sommet du cone à respectivement le Cdg à vide (déterminé ci dessus), le CdG de la masse d?eau et le CdG de la fusée en charge.
Si l?on nomme Mv, Me et Mg les masses respectives de la fusée à vide, de l?eau et de la fusée en charge, on a la relation :
Mg * Xg = Mv * Xv + Me * Xe
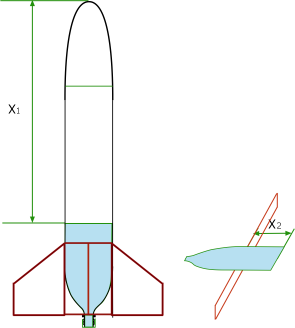
Pour déterminer le CdG de la masse d?eau, remplir d?abord la fusée de la quantité d?eau voulue, puis mesurer la distance entre le sommet du cone et la limite air-eau (X1 sur la figure ci-dessous). Dans du carton, dessiner la silhouette de la masse d?eau et rechercher son centre de gravité à l?aide d?une règle par exemple, comme sur le dessin ci-dessous.
La distance Xe sera alors égale à X1 + X2.
Le centre latéral de poussée (CLP) est le point d?application des forces aérodynamiques orientées perpendiculairement à l?axe de la fusée. En clair, s?il y a une rafale de vent, la force que va exercer ce vent sur la fusée aura son point d?application au centre latéral de poussée.
Ce centre peut être déterminé par le calcul grâce aux équations de Barrowman, c?est la méthode décrite dans le cahier technique Planète Sciences « Le vol de la fusée », donc nous n?y reviendrons pas ici.
Il est également possible de trouver ce CLP par une méthode plus rudimentaire mais néanmoins valable. Il suffit de découper dans du carton la silhouette de la fusée (entière cette fois-ci) et de rechercher le centre de gravite de cette silhouette, comme vu précédemment pour le CdG de l?eau, qui correspond sensiblement au CLP.
Le CLP doit donc être situé au moins un calibre au dessous du CDG. Le calibre est tout simplement le diamètre du corps de la fusée.
En final, il sera toujours fructueux de tester la stabilité de la fusée en réalisant un test « en vol circulaire ». C?est à dire que l?on attache la fusée à une ficelle au niveau de son centre de gravité, comme pour déterminer celui-ci. Donc la fusée doit être en équilibre comme sur la figure en haut de cette page. On la fait alors tourner autour de soi, comme une fronde sauf qu?ici on ne lâche jamais la ficelle. Si elle reste bien en ligne, perpendiculaire à la ficelle, pointe en avant et ailerons en arrière, la fusée est stable. Si au contraire elle tournoie dans tous les sens, ou pire si elle tourne ailerons en avant, alors la stabilité est à revoir.