La propulsion
Principes de base
Le principe de propulsion de toute fusée repose sur la loi de la conservation de la quantité de mouvement, connue également sous le nom de loi de l'action et de la réaction. C'est cette loi qui fait que si vous montez avec un ballon sur une planche à roulette, elle même posée sur un sol plat et bien lisse, lorsque vous lancez le ballon devant vous, vous reculez.
La quantité de mouvement d'un élément matériel est le produit de sa masse m par sa vitesse v, celle d'un système matériel est la somme des quantités de mouvement de chacun de ses éléments matériels.
La loi de la conservation de la quantité de mouvement dit :
"La quantité de mouvement d'un système matériel est nulle ou demeure constante si les forces extérieurs qui lui sont appliquées ont une résultante nulle".
Reprenons l'exemple précédent et supposons d'une part que les forces de frottement de la planche à roulette sur le sol soient nulles et que d'autres part vous êtes en équilibre et immobile. Le système matériel composé de votre personne sur la planche à roulette plus le ballon a une résultante nulle des forces extérieures qui lui sont appliquées (poids compensé par la réaction du sol) et la vitesse étant nulle, la quantité de mouvement est nulle : m*v = 0. Si vous lancez le ballon, les deux parties du système matériel que vous formez ont une quantité de mouvement qui est le produit de leur masse respective par leur vitesse. Comme il y a conservation de la quantité de mouvement du système, on a
m1*v1 + m2*v2 = m*v = 0 et donc v1 = -v2*(m2/m1)
Ce qui signifie que si le ballon de masse m2 est lancé avec une vitesse v2, l'expérimentateur sur sa planche à roulette partira en sens inverse du ballon à une vitesse v1 égale au produit de la vitesse v2 par le rapport de masse m2/m1. Si m1 = 50 kg et m2 = 1kg, v1 sera 50 fois plus faible que v2.
Donc, pour une fusée, la règle du jeu consiste à éjecter une masse de matière (gazeuse ou liquide) avec une vitesse suffisante pour propulser l'engin dans l'autre sens.
Dans une fusée à eau, la matière propulsive est de l'eau éjectée par la mise sous pression du réservoir.
Calcul de la poussée
Supposons notre fusée à eau non soumise à des forces exterieures (poids, résistance de l'air entre autres), à un instant t après le décollage, la masse de la fusée est m, sa vitesse v et la vitesse d'éjection de l'eau est v' (donc par rapport à la terre, la vitesse de l'eau est v-v').
Considérons l'instant infiniment voisin t + dt, pendant le lapse de temps très court dt, une masse dm d'eau va être éjectée, donc la masse de la fusée aura diminuée de dm, mais sa vitesse aura augmentée de dv.
La quantité de mouvement de la fusée, à ce moment, sera de (m-dm)*(v+dv), tandis que la quantité de mouvement de la masse d'eau éjectée est dm(v-v').
Comme il y a conservation de la quantité de mouvement :
(m-dm)*(v+dv) + dm*(v-v') = mv (Qté de mouvt à t+dt = Qté de mouvt à t)
en réduisant et en négligeant le terme dm*dv très petit devant les autres, on obtient :
m*dv = dm*v'
Si on appelle le débit massique d'eau q = dm/dt, on a dm=q*dt, d'où :
m*dv = q*dt*v' soit encore m*(dv/dt) = q*v'
or dv/dt est l'accelération et donc selon le principe fondamental de la dynamique m*(dv/dt) est représentative de la force générée par l'éjection de l'eau, c'est la poussée P. On voit d'après la formule ci dessus que cette poussée est proportionnelle à la masse d'eau éjectée par seconde multipliée par la vitesse d'éjection de cette eau :
P = q*v'.
Le débit massique étant la masse d'eau éjectée par seconde, c'est aussi égal au produit de la masse volumique ρ par le volume éjecté par seconde. Ce dernier est égal au produit de la surface d'éjection par la vitesse d'éjection : s*v' . d'où la nouvelle équation de la poussée :
P = ρ*s*v'2
Pour calculer la vitesse d'éjection de l'eau, nous utilisons le théorème de Bernoulli. La famille Bernoulli ayant engendré beaucoup de génies des mathématiques et de la physique, il est bon de préciser que ce théorème est dû à Daniel Bernoulli (1700-1782).
Ce théorème dit en substance que pour un liquide incompressible et non visqueux, il y a conservation de l'énergie mécanique dans l'écoulement en régime permanent et non turbulent de ce fluide. Cette énergie mécanique est la somme des trois composantes que sont les énergies cinétique, potentielle et de pression. Entre deux points 1 et 2 d'un filet fluide, on a la relation :
(v12/2*g) + p1/(ρ*g)+h1 = (v22/2*g) + p2/(ρ*g)+h2
Application à notre fusée à eau :
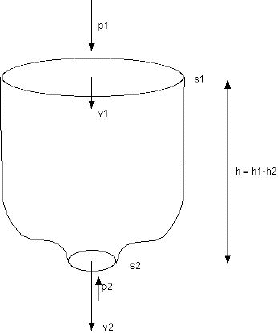
A la surface de séparation entre l'eau et l'air sous pression, à un instant donné, on a une pression p1, une surface s1 (celle du corps de la bouteille) et une vitesse v1.
A la sortie du goulot de la bouteille, au même instant, on a une pression p2 qui est la pression atmosphérique Patm, une surface s2 (celle du goulot) et une vitesse v2.
Entre les deux surfaces, on a une hauteur d'eau h qui est la différence d'altitude entre les surfaces 1 et 2.
Le liquide étant incompressible, le débit en 1 est égal au débit en 2, donc
s1*v1 = s2*v2 et v1 = v2 * (s2/s1)
Dans l'équation du théorème de Bernoulli, nous aurons alors :
((v22 * (s2/s1))2/2*g) + p1/(ρ*g)+h1-h2 = (v22/2*g) + Patm/(ρ*g)
En simplifiant, il vient :
v22 = (2/(1-(s2/s1)2))*(((p1-Patm)/ρ)+g*h)
On peut encore simplifier ce résultat en considérant que (s2/s1)2 est petit devant 1, de même que g*h est très petit devant (p1-Patm)/ρ.
l'équation devient donc :
v22 = 2*((p1-Patm)/ρ)
Si maintenant on utilise ce résultat dans l'expression de la poussée trouvée plus haut on obtient :
P = 2 * (p1-Patm) * s2
Il faut se souvenir que p1 est la pression absolue dans la bouteille, or la pression qu'on lit sur le manometre est une pression différentielle, c'est à dire p1 - Patm
Exemple numérique : soit une bouteille de 1,5 l normale, avec un goulot de 22mm de diametre, gonflée à 6 bars (607950 Pa) au manométre. la poussée au départ sera donc de :
P = 2*607950*3,14*0,022^2/4 = 462 N