Payload

Apart from the recovery system, which can use a mechanical or electronic timer, it may be interesting to take some equipment on board to measure the performance of the rocket, film the flight, make the rocket more visible or any other experiment.

Here we will see some of the most common measurements.

Altitude measurement

As soon as we launch our first water rockets, the desire to know at what altitude our achievements are quickly felt.

This measurement can be done either from the ground or using on-board electronics.

Measuring from the ground

The easiest way, even if it is not the best accurate, is the 'trigonometric gun', based on the principle below :

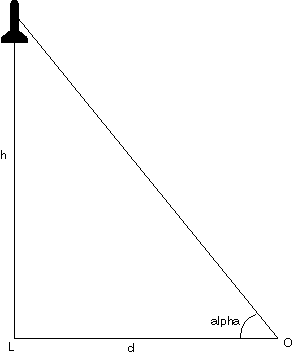
If we know the distance d between the observer O and the launcher L, we are able to calculate the height h by the formulas h = d*tg(alpha).

The less is the angle, the best is the précision, so we have to stand quit far from the launcher. Between 50 and 100m seem to be a good distance.

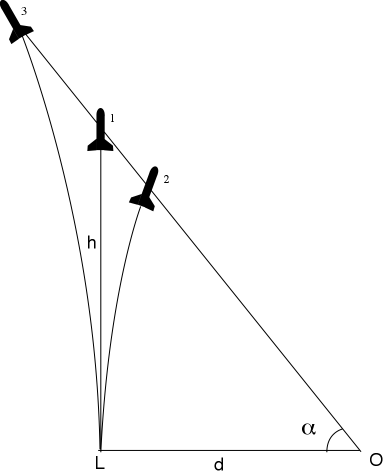
But this method has some limits. First the sighting is not very accurate, as the estimate of the apogee. Then the locking of the plumb line with the finger doesn't go in the best way for the accurate. Last but not the least, if we look for the opposite picture, we can see that if the trajectory of the rocket is not in a plan perpendicular to the axe Launcher-Observer (case of the rockets 2 and 3) the calculation is completely false.

To compensate for this issue, we must have two observers and use a little more sophisticated device. Each observer have to read 2 angles, the angle alpha as previously, but also the angle Thêta showned on the picture below.

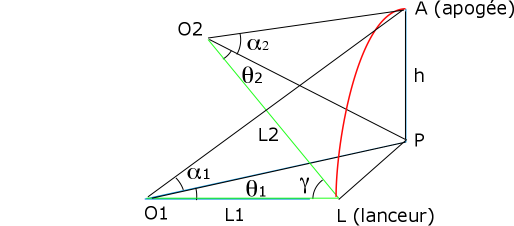
The L point is the launcher position.

The points O1 and O2 are corresponding to the positions of the 2 observers, distant respectively from L1 and L2 of the launcher.

The A point is the apogee of the rocket, while the P point is the projection on the ground of the A point.

We calculate first the coordinates of P point by the formulas :

Xp=(L1*tg(Théta1)-L2*cos(Gamma)*tg(Theta2-gamma)-L2*sin(gamma))/(tg(theta2-gamma)-tg(theta1))

Yp=tg(theta1)*Xp+tg(Theta1)*L1

Using these coordinates, we can calculate the height h either with the angle alpha1, either with the angle alpha2. The idéal is to do both calculation, the result must be the same, apart from the uncertainties of measures...

The altitude h is given by the following formulas :

h = (Yp/sin(Théta1))*tg(alpha1)

h = (Yp-(L2*sin(gamma))*tg(alpha2)/sin(gamma-théta2)

You'd be well advice to make a spreadsheet in Excel or something else or in a programmable pocket calculator to have a fast result.

You can also note down the datas and then make a geometric drawing at 1/1000 scale for example (1cm= 10m).

In this way, search first the P coordiantes by drawing the lines LO1 et LO2, then, with the angles Théta1 and théta2, the lines O1P and O2P.

On another diagram, draw again O1P and its perpendicular in P, then with the angle alpha1, draw the line O1A. to test, draw O2P and its perpendicular in P, then with the angle alpha2, draw the line O2A. In both cases, the height PA must be the same (apart the uncertainties of measures and geometric construction).

The first trigonometric gun I made, was built with a piece of broom handle, under which I glued a piece of cardboard. On this cardboard, I drew a 1/4 circle with graduation each 5°. In the center of the circle, I fix an axis around which can rotate a metal rod. At the bottom of this metal rod I put a lead ballast.

The broom handle allows to aim at the rocket, and at the apogee, I must lock the metal rod with the finger. Then I can read the alpha angle.

Here is my realization, it's a little bit "rustic" :-)

Bellow, you can see the new version which looks like more to a gun. The sight is more accurate.

The angle measure is made with a disk which is graduated each 5°. This disk is lead ballasted. When the rocket reach the apogee, I lock the disk with the trigger. Then I can read the angle in front of a marker on the gun.

Other measure method are availables, for example :

Using an altimeter which record datas inside (EEPROM for example) or transmit by radio.
At the apogee the rocket drop a "calibrated object" for which the fall down speed is constant and known, so, we have to measure the time of this object from the apogee to the ground and we know the altitude.
and probably others methods...

Measurement by on-board electronics

The easiest way is to use commercial altimeters such as:

The PerfectFlite A15K altimeter (www.perfectflite.com )

The underside

the top

This model has been replaced by the more efficient model Pnut


The underside	The top

There are many other models, unfortunately not easy to find in France, but with the internet, it is easy to get them, especially from Apogee Components (http://www.apogeerockets.com)

Nothing prevents, of course, to build your own altimeter, there are many microcontrollers incorporating analog / digital converters and enough EEPROM to record the data. Miniature pressure sensors are a little less numerous, but still accessible.

Other possible measures

Advances in electronic sensors, particularly thanks to smartphones, now allow us to have sensors tiny containing 3-axis accelerometers + 3-axis gyroscopes, even 3-axis magnetometers making it possible to trace the entire rocket trajectory. The data volume is then enough important, it will probably be necessary to provide an external EEPROM memory to the microcontroller.

Vidéo

There too, it is possible to obtain mini-cameras giving films of fairly good quality for a few dozen euros. Like these :

Of course, this is only a glimpse of what can be found. The flycamone (in blue) is a fairly old model. The two cameras on the left have a lens that looks at us, which requires a small mirror at 45 ° to film towards the ground.

But nothing forbids filming "horizontally".

While the 2 cameras on the right, keychain style, have a lens on the edge, opposite the ring, which makes it easier to shoot in the direction of the ground.

Cansat

We can very well imagine to take away in his rocket a Cansat that will be dropped at the peak. No, do not laugh, I did it. Proof:


The rocket on the ramp with the Cansat inside	The rocket after landing ...	.. and the Cansat also on the ground, a little further.

Of course, the Cansat can embed an experience. In the example above, there was nothing. The goal was simply Check the proper operation of the release of a Cansat.

For a water rocket, the enemy, it's the weight. So the more wee wanted xperiences, the more heavy and the less the rocket goes high. So, we'll have to find solutions to give more power to the rocket.