Propulsion
Basics principles
The principle of propulsion of any rocket is based on the momemtum conservation law, also known as action and reaction law. To illustrate this law, you can do the following experience : Take a ball and get on a roller skate, if you launch the ball behind you, you go backward.
The momentum of an element is the product of its mass m by its speed v, the one of a system is the sum of the momentum of each parts of its system.
The momemtum conservation law says :
"The momemtum of a system is null or stays constant if the resultant of the external forces, on this system, is null".
In the previous example, if we suppose that there is no friction force beetween the roller skate and the ground, and you are balanced and motionless. The system is composed of you, with your ball, on your skate board. The resultant of the external forces are null (the weight of your system is offset by the ground's reaction). As the speed is null, the momemtum is null : m*v = 0. If you launch the ball, the two parts of your system have a momemtum equal to the product of their respective mass by their speed. As there is system, we have : momemtum conservation of the
m1*v1 + m2*v2 = m*v = 0 and thus v1 = -v2*(m2/m1).
This means that if the ball with a mass m2 is launched with a speed v2, you, on your roller skate, will go in the opposite direction of the ball with a speed v1 equal to the product of v2 by the mass ratio m2/m1. If m1 = 50 kg and m2 = 1kg, v1 will be 50 times lower than v2.
Thus, for a rocket, the rule of the game is to eject a mass of material (liquid or gas) with a speed as high as possible to propels the rocket in the opposite direction.
In a water rocket, the material is water ejected by high pressure air.
Calculation of the thrust
Suppose our water rocket in the outer space and far from the earth, thus without external forces ( no weight and no drag forces), at the time t after the launch, the mass of the rocket is m, its speed is v and the eject speed of the water relative to the rocket is v' (thus relative to the earth, the eject speed of the water is v-v').
Consider the time infinetely close t + dt, during the small amound of time dt, a mass dm of water will have ejected, thus the mass of the rocket will have lost dm, but its speed will have gained the small amound of speed dv.
At this time the momemtum of the rocket will be (m-dm)*(v+dv), while the momentum of the ejected water is dm(v-v').
Since the momentum is conserved, we have :
(m-dm)*(v+dv) + dm*(v-v') = mv (Momentum at t+dt = Momentum at t)
if we neglect dm*dv very small relative to the others, we arrive to :
m*dv = dm*v'
If we call the the mass flow of water q = dm/dt, we have dm=q*dt, thus :
m*dv=q*dt*v' or m*(dv/dt)=q*v'
but dv/dt is the acceleration and as the Nedwton's second law of motion says m*(dv/dt) is representative to a force, generated by the ejection of the water, this is the thrust P. So, we can see that the thrust is proportional to the mass of water ejected per second and its speed of ejection :
P=q*v'.
The mass flow of water ejected per second is equal to the density of water r time the volume flow ejected per second. This last one is the product of the eject speed by the area of the nozzle : s*v'. so the new equation of the thrust is :
P = r*s*v'2
Now we have to calculate the eject speed of water and for that we have to use the theorem of Bernoulli. The Bernoulli's family had generated many genius of mathematics and physics, it's good to precise that this theorem is due to Daniel Bernoulli (1700-1782).
This theorem says that for an incompressible and non viscous fluid, the mechanical energy is conserved in steady fluid flow. This mechanical energy is the sum of three components : The kinetic energy, the potential energy and the pressure energy. Between two points 1 and 2 of a steady-flowing, non-viscous and incompressible fluid, we have the equation :
(v12/2*g) + p1/(r*g)+h1 = (v22/2*g) + p2/(r*g)+h2
Application to our water rocket :
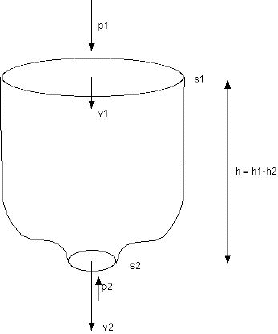
At the area 1 between the water and the air, we have a pressure p1, an area s1 (those of the body of the bottle) and a speed v1.
At the end of the neck of the bottle, we have a pressure p2 which is the atmospheric pressure Patm, an area s2 (those of the neck) and a speed v2.
Between these two areas we have a height of water h which the difference of altitude between the two areas 1 and 2.
The liquid being incompressible, the flow rate in 1 is the same as the flow rate in 2, thus
s1*v1 = s2*v2 and v1 = v2 * (s2/s1)
Then in the Bernoulli's equation, we will have :
((v22 * (s2/s1))2/2*g) + p1/(r*g)+h1-h2 = (v22/2*g) + Patm/(r*g)
We can simplify, so :
v22 = (2/(1-(s2/s1)2))*(((p1-Patm)/r)+g*h)
We can simplify this result because (s2/s1)2 is very smaller than 1, and then g*h is very smaller than (p1-Patm)/r.
Thus the equation becomes :
v22 = 2*((p1-Patm)/r)
Now if we use this result in the expression of the thrust that we find previously, we obtain :
P = 2 * (p1-Patm) * s2
Where p1 is the absolute pressure in the bottle, that is the pressure we can read on the gauge plus the atmospheric pressure. Thus p1 - Patm is the pressure gauge.
Numeric example : Let a normal bottle of 1,5 l, with a diametre neck of 22mm, be pressurized at 6 bars (607950 Pa) at gauge. The thurst at the beginnig will be :
P = 2*607950*3,14*0,0222/4 = 462 N