Stability
We have seen the page on aerodynamics that it was necessary to have the center of pressure under the center of gravity. What we don't have seen however, is how to determine where are the centers of gravity and pressure, nor how to evolve their position if they are not correct. This is what we will see here.
Water rockets have a few features that it must be underlined.
'Propulsive mass' is related much larger than for powder rockets, for example a water rocket made up a bottle of 1.5 l will weigh about 100 g empty, but filled with 1/3 of water volume, it will weigh 600g. A rocket with engine type E will weigh approximately 1 kg for 40g of powder. This explains the great acceleration of the water rockets.
Also, this means that the centre of gravity of the rocket will move during the propulsion phase. It goes forward, what is rather favorable for the stability, fortunately for that matter because a water rocket during take-off, so with all the water inside, has its centre of gravity very low (roughly this is the centre of gravity of the mass of water) so to have a center of pressure lower at least in diameter, requires very large fins or / and a very low position.
In practice, the phase of propulsion is generally very short, a few hundredth of seconds, it is not absolutely necessary to have a stable rocket at take-off. First, the water will ejected very quickly so the duration of instability will be very short and if there is a disturbance at takeoff, very quickly the rocket will find its trajectory, on the other hand the acceleration is huge which means that speed is quickly important so the aerodynamic effect of the fins will be quickly noticeable.
However, we must keep in mind that take-off can be perilous and it is therefore imperative to observe the basic rules of safety during the launches. This fact also argues for a guide of the rocket at liftoff.
Finally, the duration of the propulsion phase depends on the diameter of the nozzle, the smaller the diameter is, more the time will be long and thus the period of great instability. If the diameter of nozzle will be weak, it will be necessary to design a stable machine even in charge (with water), which unfortunately cannot be done only at the detriment of performance.
But life is thus made, everything is a matter of compromise...
Le grand principe, qui permet de déterminer si une fusée sera stable ou non, dit que :
Le centre de gravité doit se trouver au dessus du centre latéral de poussée, d?au moins un calibre.
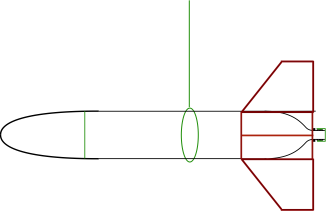
Le centre de gravité est le point d?application du poids, il est donc facile de déterminer expérimentalement sa position pour la fusée à vide. Il suffit en effet de suspendre la fusée, à l?aide d?une ficelle passée autour de son fuselage et de rechercher le point où elle restera horizontale. La position de la ficelle indiquera celle du centre de gravité (CdG).
Malheureusement cette technique ne permet pas de trouver le centre de gravité avec l?eau à l?intérieur puisque celle-ci se répand horizontalement. Il faudra donc le calculer , sachant que :
si l?on appelle Xv, Xe et Xg les distances du sommet du cone à respectivement le Cdg à vide (déterminé ci dessus), le CdG de la masse d?eau et le CdG de la fusée en charge.
Si l?on nomme Mv, Me et Mg les masses respectives de la fusée à vide, de l?eau et de la fusée en charge, on a la relation :
Mg * Xg = Mv * Xv + Me * Xe
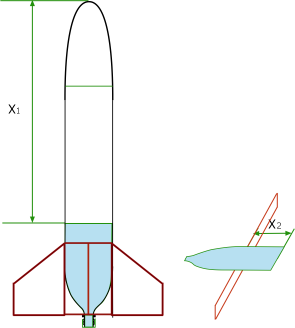
Pour déterminer le CdG de la masse d?eau, remplir d?abord la fusée de la quantité d?eau voulue, puis mesurer la distance entre le sommet du cone et la limite air-eau (X1 sur la figure ci-dessous). Dans du carton, dessiner la silhouette de la masse d?eau et rechercher son centre de gravité à l?aide d?une règle par exemple, comme sur le dessin ci-dessous.
La distance Xe sera alors égale à X1 + X2.
Le centre latéral de poussée (CLP) est le point d?application des forces aérodynamiques orientées perpendiculairement à l?axe de la fusée. En clair, s?il y a une rafale de vent, la force que va exercer ce vent sur la fusée aura son point d?application au centre latéral de poussée.
Ce centre peut être déterminé par le calcul grâce aux équations de Barrowman, c?est la méthode décrite dans le cahier technique Planète Sciences « Le vol de la fusée », donc nous n?y reviendrons pas ici.
Il est également possible de trouver ce CLP par une méthode plus rudimentaire mais néanmoins valable. Il suffit de découper dans du carton la silhouette de la fusée (entière cette fois-ci) et de rechercher le centre de gravite de cette silhouette, comme vu précédemment pour le CdG de l?eau, qui correspond sensiblement au CLP.
Le CLP doit donc être situé au moins un calibre au dessous du CDG. Le calibre est tout simplement le diamètre du corps de la fusée.
En final, il sera toujours fructueux de tester la stabilité de la fusée en réalisant un test « en vol circulaire ». C?est à dire que l?on attache la fusée à une ficelle au niveau de son centre de gravité, comme pour déterminer celui-ci. Donc la fusée doit être en équilibre comme sur la figure en haut de cette page. On la fait alors tourner autour de soi, comme une fronde sauf qu?ici on ne lâche jamais la ficelle. Si elle reste bien en ligne, perpendiculaire à la ficelle, pointe en avant et ailerons en arrière, la fusée est stable. Si au contraire elle tournoie dans tous les sens, ou pire si elle tourne ailerons en avant, alors la stabilité est à revoir.